度数分布を表すグラフとして利用されるヒストグラムは、数字で表された分布表を図に変換して分かりやすくするツールです。
ヒストグラムを利用することで、プレゼンや会議などで資料の内容を相手に伝えやすくなり、自身の理解力も助けます。
ヒストグラムを活用するために、ヒストグラムの書き方や見方、よく混同される棒グラフとの違いなどを解説していきます。
目次
ヒストグラムとは?
ヒストグラムとは、ある特定のデータを区間ごとに区切り、各区間の個数や数値のばらつきを棒グラフに似た形の図で表現するグラフです。ヒストグラムを作成することで、数値で集めた度数分布表を視覚的に分かりやすく表現できます。
ヒストグラムは、製造現場などで数値解析に使用される「QC七つ道具」の一つとされています。別名「度数分布図」「柱状グラフ」などとも呼ばれる、度数分布を図で表すグラフのことです。
度数分布表を元に数値を図に変換します
| 度数分布表:例「300個のりんご収穫時の重量分布」 | |||||
| 計測結果 | 度数分布表 | ||||
| 291.4 | 303.1 | 291.1 | 305.5 | 重量(階級) | 数量(度数) |
| 289.8 | 297.2 | 299.9 | 295.0 | ~280g | 5個 |
| 299.6 | 295.8 | 296.1 | 287.6 | 281-285g | 20個 |
| 291.9 | 302.5 | 297.4 | 297.2 | 286-290g | 46個 |
| 274.5 | 300.5 | 305.5 | 298.8 | 291-295g | 75個 |
| 297.8 | 307.8 | 296.2 | 306.0 | 296-300g | 72個 |
| 295.7 | 291.7 | 301.8 | 290.1 | 301-305g | 37個 |
| 295.5 | 285.9 | 299.8 | 301.9 | 306-310g | 30個 |
| 291.2 | 291.0 | 296.6 | 292.3 | 311-315g | 9個 |
| 302.6 | 303.3 | 294.6 | ~~~ | 316-320g | 5個 |
| 287.5 | 312.7 | 合計 | 300個 | 320g~ | 1個 |
度数分布表とは、収集したデータをある幅ごとに区切って、その中に含まれるデータの個数を見るための数値をまとめた表です。
上記の表では、収穫時のりんごの重量が左側に記録してあり、その結果を元に右側の度数分布表に重量のバラつきをまとめています。
このような度数分布表だけでも、データの分散度合いや中央値を知ることができますが、ヒストグラムを作成すれば、数値だけではなく視覚的に理解しやすくなります。
ヒストグラムの横軸(x軸)は「階級」を表現
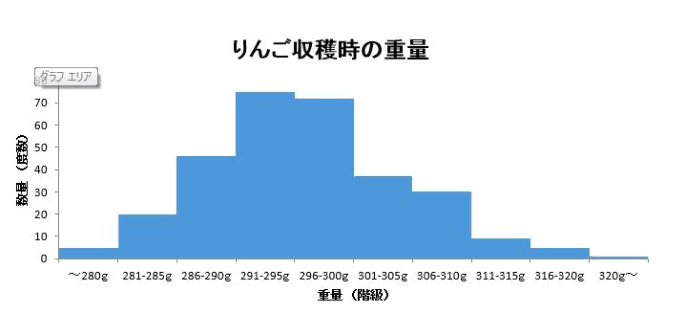
先ほどの例題を元に作成したヒストグラムが上記の図です。
数値でデータの分布を表現した度数分布表よりも、一目でバラつきや中央値が認識しやすいことがわかるのではないでしょうか?
ヒストグラムでは、横の軸(x軸)に記載する数値を「階級」と呼び、データを区切った区間を記入します。今回の例題では、りんごの重量を300g(グラム)を中心として、5gごとに区切って階級を定めました。
ヒストグラムの縦軸(y軸)は「度数」を表現
同様に、ヒストグラムの縦軸(y軸)には、各区間に含まれるデータの数量を記入します。ヒストグラムの縦軸(y軸)は「度数」と呼ばれ、今回の例題では、重量の各階級に含まれるりんごの数を記載しました。
ヒストグラムと棒グラフの違い
これまでの例を見ると、ヒストグラムと棒グラフはとてもよく似ていることがわかります。数字の大きさを棒状の長方形で表しているのはどちらも同様です。
ですが、ヒストグラムでは、横軸の階級に連続した順番があります。あくまでも、一つの連続したデータの度数の分布を伝えるツールがヒストグラムです。
一方の棒グラフは、一つひとつの棒グラフが表す内容はそれぞれ独立した意味を持っているという違いがあります。各棒グラフは対等な関係であり、比較・対象するために用いられます。
例えば、上記の例題では、りんごの重量の度数分布を伝えるためにヒストグラムを使っています。横軸の階級は~280gから320g~まで、連続した意味を持っています。
一方、果樹園で取れたりんご、みかん、メロン、すいか、オレンジなどの平均重量を棒グラフで伝える場合は、横軸が各フルーツの名前になり、縦軸が重量の平均値になります。
このような棒グラフでは横軸の順番は、作成者が自由に並べ替えられます。りんごの横にみかんを並べようがメロンを並べようが自由です。各グラフの長方形ごとに独立しており、他の長方形とは連続した関係性がありません。
グラフの表現方法としても、ヒストグラムは各階級の長方形同士をくっつける事によって、連続した意味合いがあることを表現しています。一方の棒グラフは、各データを表す長方形同士の間に間隔が空いていることが特徴です。
ヒストグラムの見方
数値解析などに利用されているヒストグラムでは、その形状によって呼び名が定められています。呼び名以外にも、ヒストグラムの見方によって発見できる事柄に違いがありますので、各ヒストグラムの形について紹介します。
左右対称型

工場で作られる同じ部品の規格について、ヒストグラムを作成する際など、一般的に良く見られる形です。階級の中心部が一番多く、左右対称に度数の数値が分かれています。
例えば、正規の製品サイズが最も大きい数値になっており、許容値の範囲内で左右対称型にサイズがバラけていれば、安定した加工が行われているなどの情報が理解できます。
はなれ小島型
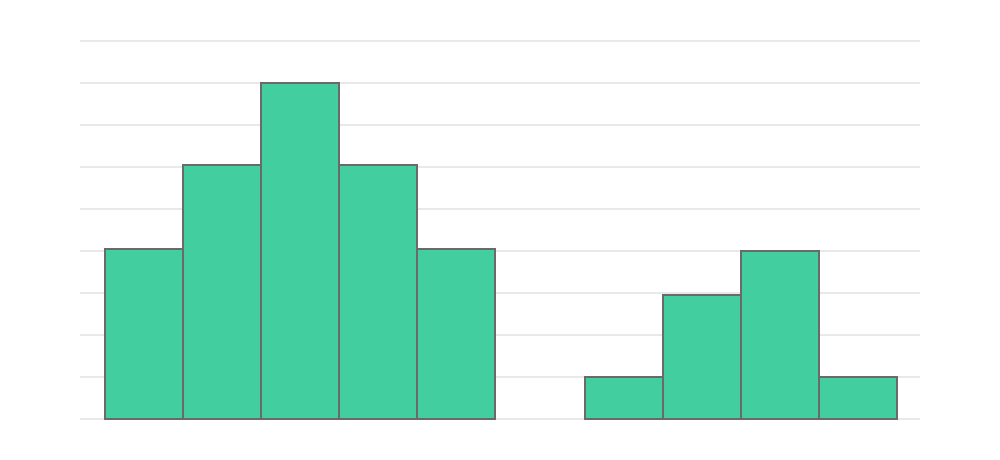
はなれ小島型は、中央値とは離れた場所にも少量のデータが見られる形のヒストグラムです。
異なったデータの混入や測定の誤りなどの可能性があります。離れた山でもある程度の数量がある場合は、本来予測していない何かしらの要因によって、作業や調整をミスしている可能性も考えられます。
二つ山型
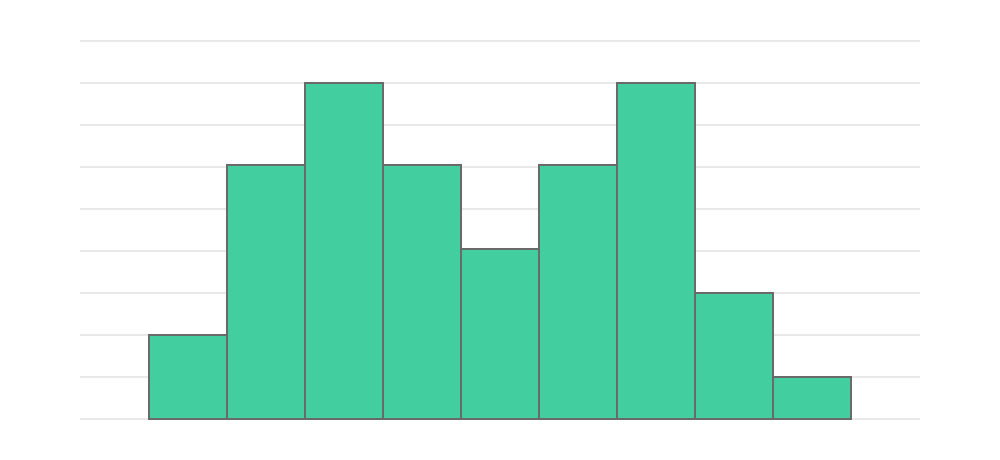
二つ山型のヒストグラムは、中央値よりも左右の数量が多くなっている形です。
通常であれば左右対称型になるヒストグラムで二つ山形になった場合は、中央値が違っているデータの混入が考えられます。他にも機械、作業員などの異なる要因が交じり合っている度数分布表を使った場合に、二つ山型になる可能性も存在します。
二つ山型になっている要因ごとに度数分布表のデータを分けて、再度ヒストグラムを作成することで、左右対称型のデータになる可能性があります。
櫛歯型
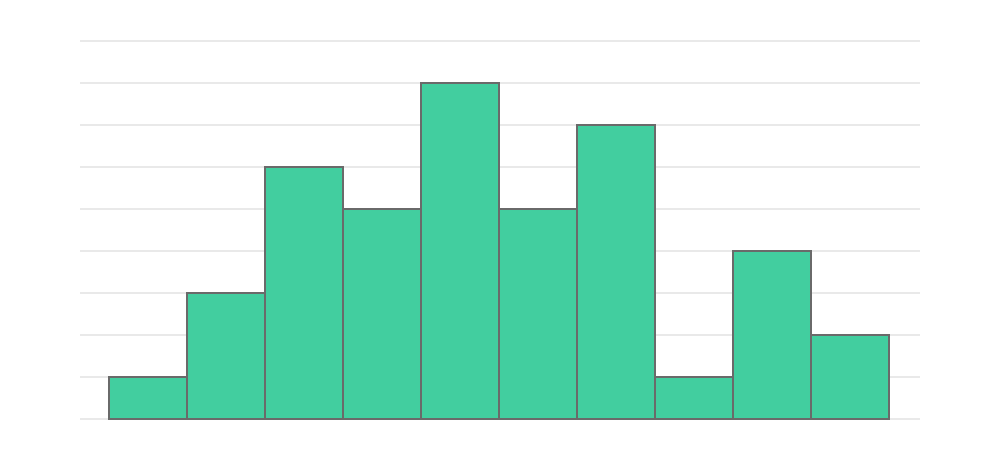
櫛歯型のヒストグラムはデータが山形でなく、でこぼこな形になっているものです。
度数分布表のデータの数量が少ない場合や、各階級の幅を狭く設定している際などに良く見かけられます。ヒストグラムに記載するデータの全体数量を多くしたり、定める階級の幅を大きくしたりすることで、山形のヒストグラムに変わる可能性があります。
歪みがある形
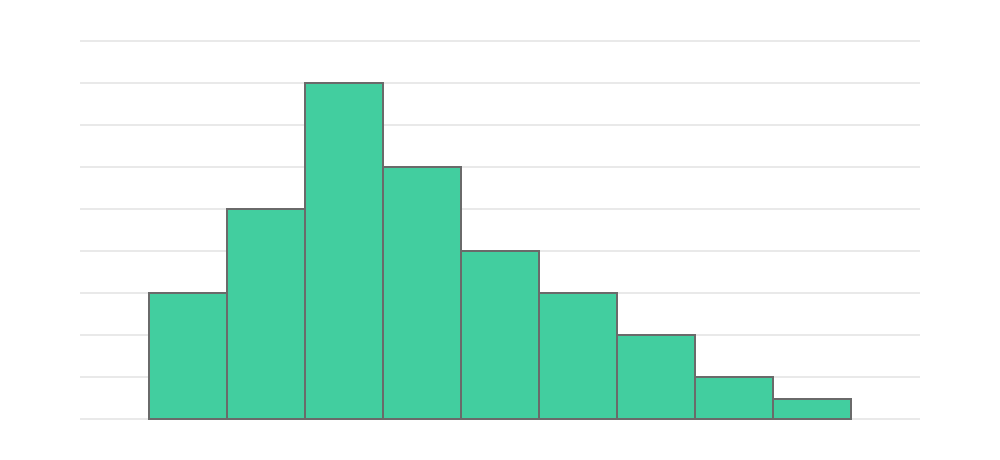
歪みがある形は、山の左右どちらかの裾の一方が伸びた形のヒストグラムです。例えば、計測するデータの上限を定めないポワソン分布などでは正常な形です。
ただし、データのゆがみが不自然な場合は、裾が延びている箇所に何かしらの制限があって度数が伸びていない可能性も考えられます。
上記のようなヒストグラムの見方を知ることで、数値解析によってデータの整合性や異常を発見できますので、覚えておきましょう。
ヒストグラムの書き方
ヒストグラムの概要や見方を紹介した後は、ヒストグラムの書き方について解説していきます。
度数分布表を作成する
| 度数分布表:例「300個のりんご収穫時の重量分布」 | |||||
| 計測結果 | 度数分布表 | ||||
| 291.4 | 303.1 | 291.1 | 305.5 | 重量(階級) | 数量(度数) |
| 289.8 | 297.2 | 299.9 | 295.0 | ~280g | 5個 |
| 299.6 | 295.8 | 296.1 | 87.6 | 281-285g | 20個 |
| 291.9 | 302.5 | 297.4 | 297.2 | 286-290g | 46個 |
| 274.5 | 300.5 | 305.5 | 298.8 | 291-295g | 75個 |
| 297.8 | 307.8 | 296.2 | 306.0 | 296-300g | 72個 |
| 295.7 | 291.7 | 301.8 | 290.1 | 301-305g | 37個 |
| 295.5 | 285.9 | 299.8 | 301.9 | 306-310g | 30個 |
| 291.2 | 291.0 | 296.6 | 292.3 | 311-315g | 9個 |
| 302.6 | 303.3 | 294.6 | ~~~ | 316-320g | 5個 |
| 287.5 | 312.7 | 合計 | 300個 | 320g~ | 1個 |
ヒストグラムを作るには、度数分布表を作成しなければなりません。はじめに分布を計測するデータを一つひとつ個別で記録していきます。
例えば、今回利用した例題の場合は、左側の青色の部分にりんごの重量を一つひとつ計測して300個ほど記録しています。
次に、収集したデータを元に、ヒストグラムの横軸である階級を定めます。上記の度数分布表では、300個計測した結果を元に280g未満のりんごから、5g間隔で320g以上までの10階級に分別しています。
定める階級は、5gごとに10個の階級であったり、10gごとに5個の階級であったりなど、作成者の見やすいように間隔(階級)を定めてください。その後、集めた個別のデータを一つひとつの各階級ごとに振り分けて度数分布表を作成します。
「横軸」と「縦軸」を決める

度数分布表を作成した後は、ヒストグラムで利用する「横軸」と「縦軸」を決定します。
「横軸」には、度数分布表で定めた階級を入力してください。
「縦軸」には、度数分布表を作成した結果、一番度数が集まった場所の数値が分かる範囲でメモリを決定します。今回の例題では、291-295gのりんごが75個と一番多い結果になりましたので、度数のメモリの最大値を80個に設定しました。
表の値をヒストグラムに入力する
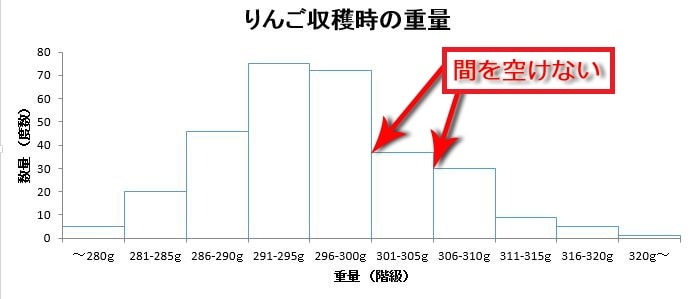
ヒストグラムの縦軸と横軸を定めたら、各階級ごとに度数分布表でまとめた数値(度数)を長方形のグラフで記入していきます。
ヒストグラムは、各長方形の間を空けないことで連続したデータの分布を表すことを伝えています。そのため、作成する際には、棒グラフのように各長方形の間を空けないように記載しましょう。
まとめた情報はヒストグラムでわかりやすくプレゼンしよう
ヒストグラムの書き方や見方、棒グラフとの違いなどを解説しました。ある項目に見られるバラつきを他者に伝える際には、数値だけの表よりもヒストグラムを作成して視覚的にわかりやすくしたほうが説得力があります。
プレゼンや学習の際に度数分布表をヒストグラムに直せば、メンバー全員の理解力が深まります。書き方や見方を学んで、ヒストグラムを活用していきましょう。

