数値解析に利用されている「QC(品質管理)7つ道具」の一つである散布図は、2つの項目の間にある相関関係を探し出すのに役に立つグラフです。
現在、品質管理などに利用しているデータが不十分と感じている方であれば、新たな管理基準を見出すために散布図の知識が必要になります。
散布図を上手に利用することで、今まで気づいていなかった管理基準に気づけるようになります。そのため、今回は散布図を作成する目的や書き方、見方や上手な使い方を解説します。
目次
散布図 とは?
散布図とは、あるデータを元にして縦軸と横軸の2つの項目で量を計測し、分布を表現するために使うグラフのことです。縦軸と横軸のメモリを元に、データが該当する場所に点をプロット(打点)することでグラフに情報を書き込んでいきます。
散布図からわかること
散布図からわかることは、あるデータに関して、縦軸と横軸のそれぞれの要素に相関関係があるのかどうかです。
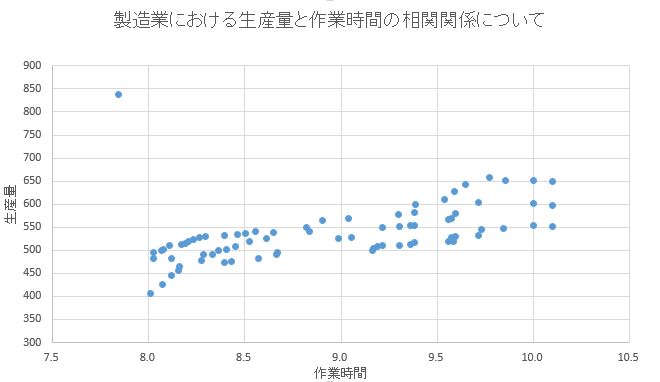
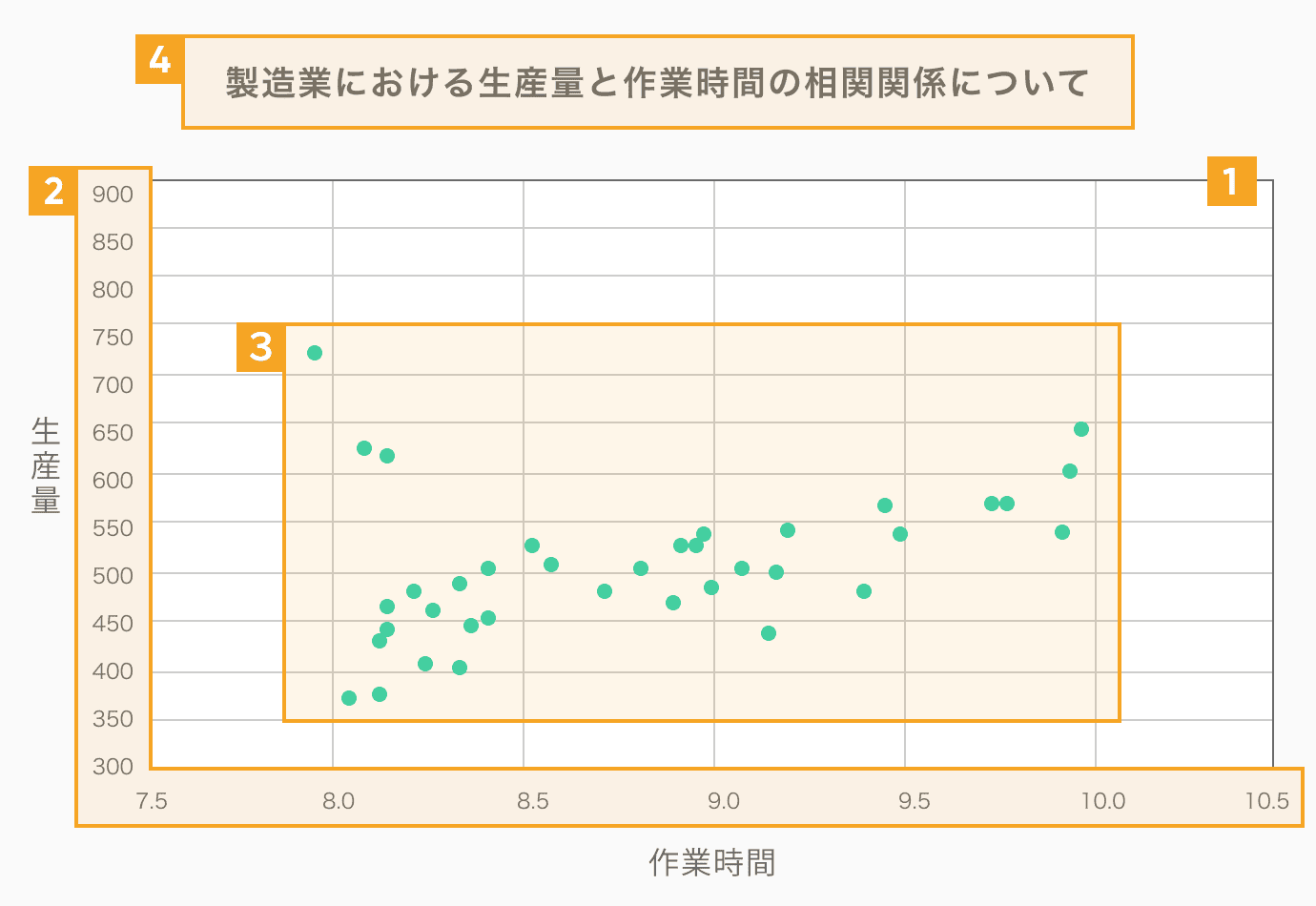
例えば、上記の表では、ある製造業において1日に生産する製品の個数を縦軸に記入し、従業員の作業時間を横軸に記載しています。そうすることで従業員の作業時間と製品の生産量について、相関関係を見出そうとしています。
散布図を見れば一目瞭然ですが、従業員の作業時間が増えると共に、製品の生産量も増えていることがわかりますよね。
その他にも、散布図ではまとまっているデータから外れた特異点もわかります。特異点は、元になっているデータが間違っている可能性が高いですが、なかにはまだ気づいていない要因により特異な条件になっている可能性も考えられます。
上記の表でも、左上に一つだけはぐれている点があります。今回の例題では、作業時間を短くするために他の人員に手伝ってもらいながら、2人体制で生産した日のデータが混入している結果でした。
このように、現在あるデータの整合性も散布図を作成することで気づく場合も存在します。
また、上記の例題では、作業時間が9時間45分ごろから10時間に近づくにつれて、製品の生産量が横ばいになっていることもわかります。このようなデータから、いくら生産量が欲しくても9時間30分以上の労働は効率が上がらないということも理解できます。
相関関係と因果関係
散布図を利用するにあたり、相関関係と因果関係の違いについて知っておいた方が良いでしょう。相関関係とはあくまで、それぞれの要素の変動がどう関係しているかを示すものであり、どちらかが原因でどちらかが結果であるとは限りません。対して因果関係とは、片方の要素がどのようにもう片方の要素に影響を与えているかを示す、原因と結果の関係です。相関関係があったとしても因果関係があるとは限らない点に注意が必要です。
上記の例題では作業時間が9時間30分を越えると効率が上がらないという相関関係が見出されましたが、この関係がそのまま、作業時間と効率の因果関係を示すものではありません。例えば、作業員の作業時間が9時間30分を越える時間にちょうど工場の空調が切られる規則があったとしたらどうなるでしょうか。作業環境が悪化し、効率も上がらなくなるのではないでしょうか。もしこのような環境であった場合、効率が上がらない真の原因は空調をオフにしたことによる作業環境の悪化であり、作業時間ではありません。
このように、相関関係は万能ではありません。データから見出した相関関係を妄信せず、品質管理の道具の一つとして扱うことが重要です。
散布図を作る目的
散布図は、「気温」と「消費電力」の関係性であったり、「材料の強度」と「加工に必要な熱量」であったり、一方の要素に対してもう一方の要素がどう変動するのかを調べることができます。
特定の2つの要因の相関関係を調べることで、
- データに影響を与えている要因を特定する材料にする
- 最適な環境を見出す
- 現状の方法よりも簡単でコストが必要ない管理方法を発見する
ということが目的になります。
散布図に見られるパターンを解説
散布図にはいくつかのパターンが存在します。そのパターンごとに2つの量の間に相関関係があるのかどうか判断できますので、例を元にどのようなパターンがあるのか解説します。
散布図パターン1:正の相関
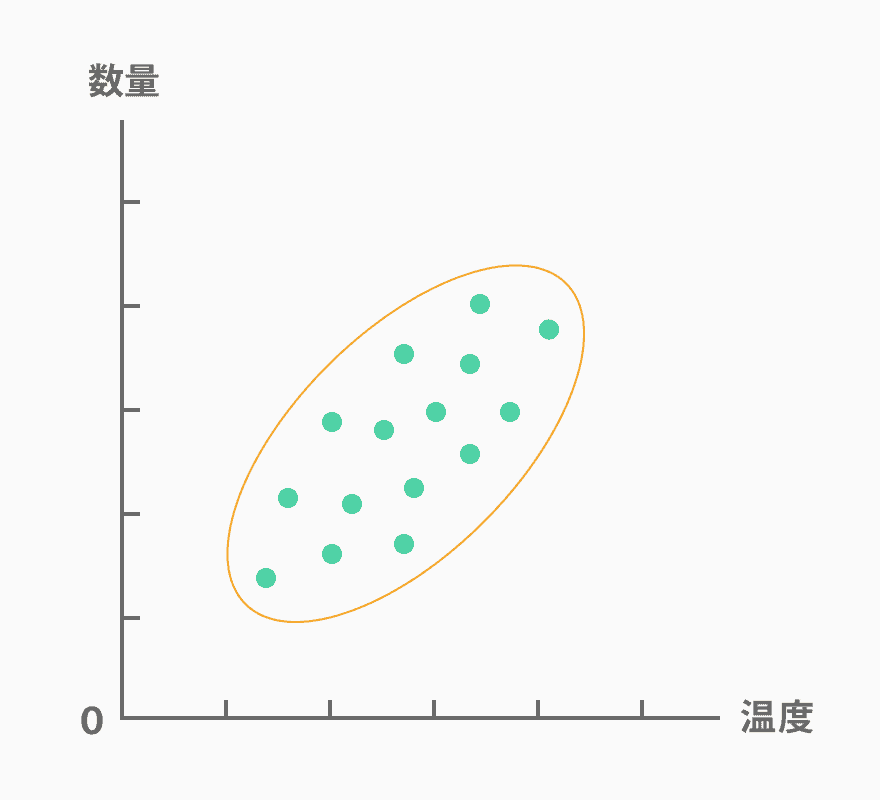
正の相関とは、一方の要因の数値が大きくなると、他方の要因の数値も大きくなる相関関係のことです。例えば、気温が熱くなると冷たい飲み物が消費されるというような場合は、このような形が見られます。
散布図パターン2:負の相関
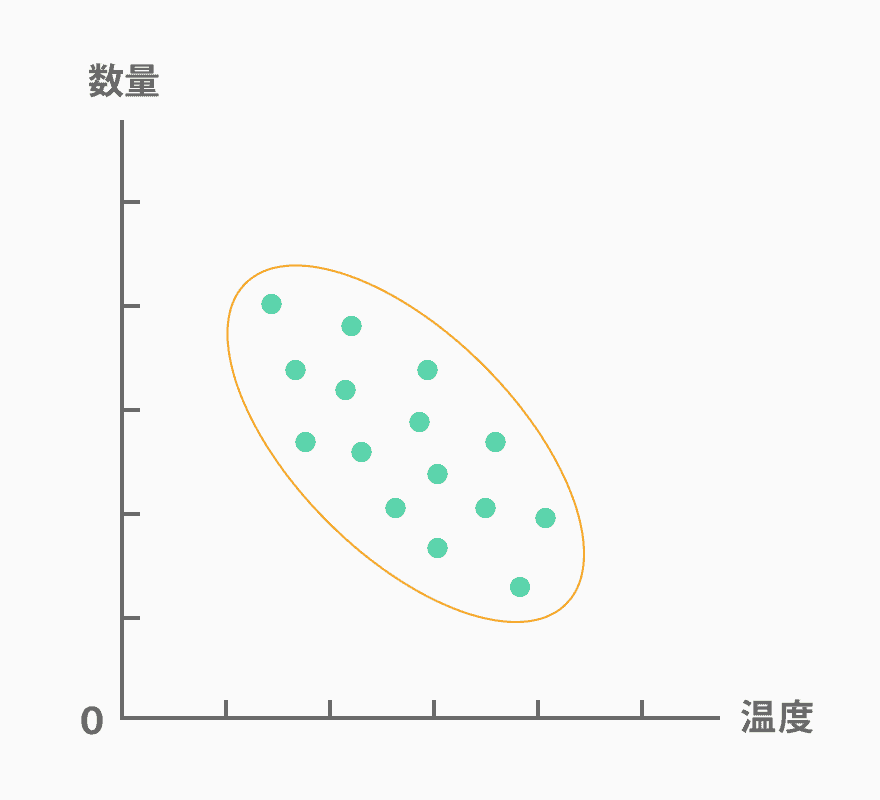
負の相関とは、正の相関とは逆に、一方の要因の数値が大きくなると他方の要因の数値が少なくなる相関関係のことです。例えば、気温が低くなると暖かい飲み物を飲む人が増えるというような場合に見られます。
散布図パターン3:相関がない
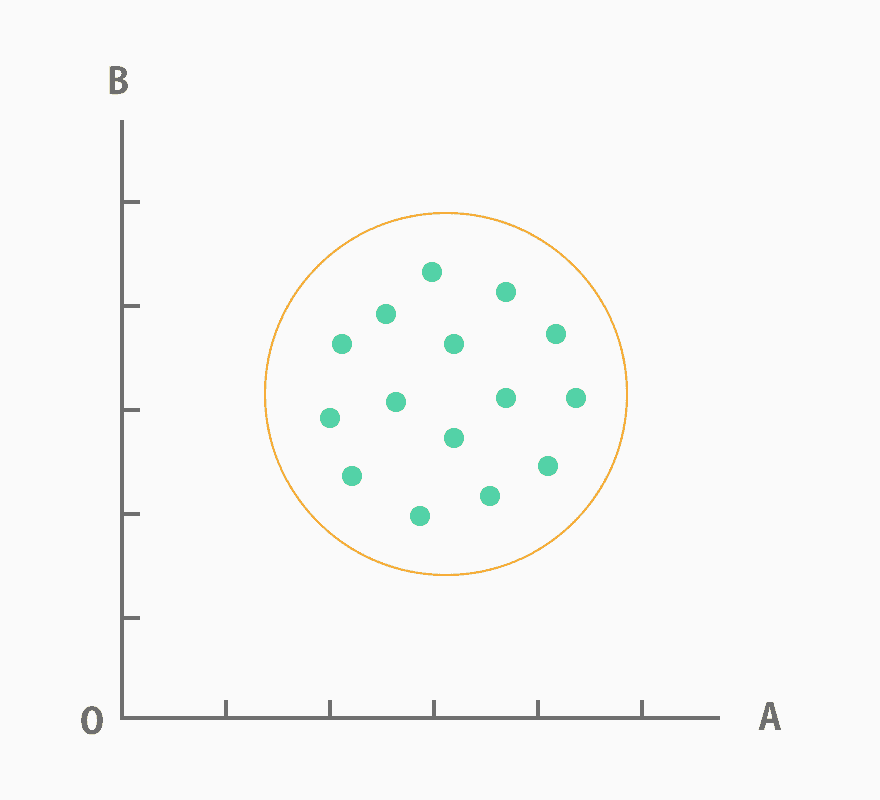
相関がない散布図のパターンとは、各データのプロットが図全体にバラバラになっているものです。
例えば、AとBの2つのサイコロを転がした時に、Aのサイコロの出目によりBのサイコロの出目が変化することは考えられません。このように、一方の要素と他の要素の間に何の関係性もない散布図では、上記のような形になります。
散布図の書き方

散布図の概要や作る目的、見られるパターンを解説した後は、散布図の書き方について手順を追って解説していきます。
散布図の書き方①:相関関係を調べるデータを用意する
散布図を作成するためには、何かしらの関係性が存在すると思われるデータを2つ用意しなければいけません。
2つのデータが要因(原因)と特性(結果)を表したものならば、要因を横軸に、特性を縦軸に入力してください。今回の例題の場合は、従業員の作業時間(原因)で製品の生産量(結果)が変化していますので、作業時間を横軸に生産量を縦軸に入力しています。
また、用意するデータ量があまり少ないと相関関係を見出せない場合も考えられます。相関関係が見出せない場合はデータ数量を再検討してみるのも良いでしょう。もちろん、求める精度に応じてあらかじめ収集するデータ数量を検討しておくことも重要です。必要なデータ数量に関しては様々な統計学的手法が存在します。
散布図の書き方②:縦軸と横軸の数量を決める
データを用意した後は、一つひとつのデータをプロット(打点)するための図を作成していきます。集めたすべてのデータがプロットできる範囲を見つけ出し、メモリを縦軸、横軸に入力してください。
例えば、先ほどの例では、横軸の作業時間は最低8時間、最大10時間10分でした。そのため、横軸のメモリには7時間半から10時間半のメモリを30分刻みで利用しています。
同じように縦軸も、最低個数である405個から最大の839個までが収まるメモリを利用しています。なおかつ、見やすい形にするためメモリの最低値と最大値に余裕を持たせました。
散布図の書き方③:プロット(打点)する
すべてのデータが収まるメモリを決定したら、集めたデータを一つひとつプロットしていきます。縦軸と横軸で該当する値を探り、交差する点に点を打っていきましょう。
同じ場所に点を打つ場合などは、すぐ横にプロットしたり、一度打った点を二重丸で囲ってみたりなど分かりやすいように工夫してください。
散布図の書き方④:散布図を作成した目的を記入する
集めたデータすべてをプロットした後は、作成した散布図で何が分かるのかを相手に伝わるように付属する情報を入力してください。
今回の例は、作業時間に対する生産量の増加を理解するためのシンプルな分布図です。そのため、図のタイトルにて図を作成した目的を伝えています。
ただし、散布図に記入する付属情報は、製品名や工程名、図を作成した人物の名前、データを計測した期間などが記入してあるほうが伝わりやすい場合も多いです。伝える内容や相手ごとにわかりやすいよう付属情報を記入しましょう。
以上の情報を図にまとめたものが散布図になります。
層別する散布図の書き方について
散布図は、記載するデータを層別することで、より詳細に相関関係が理解できるようになります。
実は、一見すると相関関係がない散布図に見えても、なにかしらの情報が足りずに関係性を見出せていないこともあるのです。
根拠がありデータを収集して散布図を作成している場合は、相関関係が見出せない散布図になったとしてもあきらめるのはまだ早いです。層別することで今まで見えていなかった情報が手に入る可能性もあります。
層別とは
層別とは、あるデータの母集団をなんらかの基準でいくつかの層に分けることをいいます。散布図においては、上記の表のように層別した要素で色分けする方法を使います。
例えば、年齢、地域、時間帯、原材料などなど、集めたデータをさらに細分化できる要素を見つけてみましょう。そして、色分けしてみると、今まで見えてこなかった相関性が浮き上がる場合も多いです。
層別に使える要素
層別は、まずはじめにどのような要素を追加して層別するのかをしっかりと決めることが重要です。確実な方法として数値のような誤解のしようがない基準にすると良いでしょう。
逆に、曖昧な要素を層別に使ってしまうと、出来上がった散布図の精度も曖昧になってしまいます。
層別の具体的な例は、
- 時間(時、日時、午前・午後、日中・夜間、週、月、季節など)
- 人(年齢、勤続年数、男女、勤務体系、チームなど)
- 素材(原材料、主成分、取引業者、メーカー、ロットなど)
- 加工方法(温度、速度、圧力、作業手順など)
- 利用する機械(号機、年式、ライン、使用年数、付属品など)
- 測定する方法(計測機器、測定者、検査方法など)
- 環境(地域、天候、湿度、粉塵など)
などが利用できます。
相関関係が明確な散布図も層別してみよう
散布図を層別することでメリットがあるのは、相関関係が曖昧な散布図だけではありません。
正の相関や負の相関がすでに分かっている散布図においても、層別することで新たな発見が見つかります。
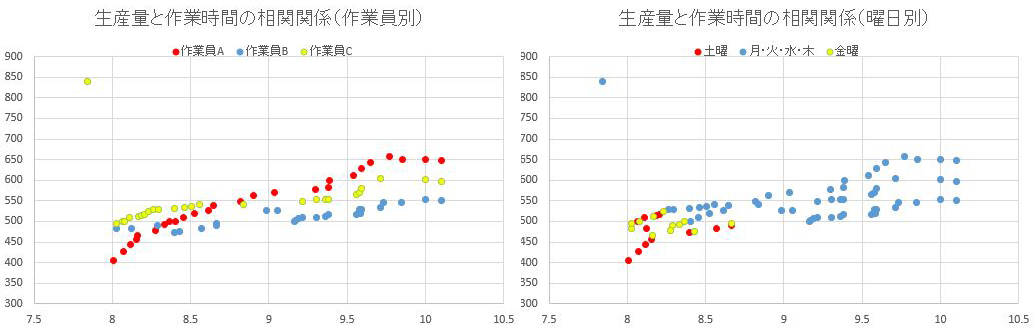
例えば、今回利用した製品の生産数と作業員の労働時間を表す散布図においても、層別することで新たな情報が手に入ります。
上記左側の表は、例題の散布図を「作業員ごと」に層別したものです。3名の従業員を別々にしてみると、赤色で記載した作業員Aは作業時間と生産数の比率が他の二名よりも右上がりな事が分かります。
また、右側の図は、月・火・水・木曜日と、金曜日、土曜日に例題を層別しています。層別した散布図をみると、疲れがたまる週末には効率が悪くなっていることが発見できました。さらに、金曜日よりも土曜日の方が作業効率が悪いことが分かります。
このように、層別は、すでにある散布図のデータからより詳細な情報を取り出すことに役立ちます。
散布図は詳細なデータを使うほど効果があります
散布図の概要や作成する目的、書き方を紹介しました。また、散布図の見方やパターンを解説し、より詳細にデータを分類できる層別についても記載しています。
散布図は、2つの異なる大きさや量を参考にすることで、2つの要素の間の相関性が理解できる便利なツールです。
さらに層別することで、今まで気づいていなかった管理方法にも可能性が見出せることもありますので、是非利用してみましょう。

